권철민 저, '파이썬 머신러닝 완벽 가이드', 2019.02.28
내 맘대로 요약 공부 중(문제시 비공개 및 삭제)
최초 작성일 2020.12.27
8.1 회귀(Regression)
- 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법
- 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법
- Y = aX1 + bX2 + cX3 …(Y: 종속변수 / X1, X2, X3: 독립변수 / a, b, c: 회귀계수)
- 즉, 머신러닝 회귀 예측은 최적의 회귀계수를 찾아내는 것(방정식 찾기)
- 분류(Classification)는 이산형, 회귀(Regression)는 숫자형
| 독립변수 개수 | 회귀 계수의 결합 |
| 1개: 단일 회귀 | 선형: 선형 회귀 |
| 여러 개: 다중 회귀 | 비선형: 비선형 회귀 |
- 일반적으로 선형 회귀를 가장 많이 사용
- 일반 선형 회귀: 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화하도록 회귀계수를 최적화, 규제(Regulation) 없음
- 릿지(Ridge): 선형 회귀 + L2규제, 상대적으로 큰 회귀 계수 값의 영향도를 감소시키기 위해 회귀 계수 값을 작게 함
- 라쏘(Lasso): 선형 회귀 + L1규제, 영향력이 작은 피처의 회귀 계수를 0으로 함
- 엘라스틱넷(ElasticNet): 선형 회귀 + L1규제 + L2규제
- 로지스틱 회귀(Logistic Regression): 분류에 사용되는 선형 모델
8.2 단순 선형 회귀
- 단순 선형 회귀: 독립변수 1개, 종속변수 1개(즉, 직선 형태의 관계)
- Y=aX1 + b(독립변수: X1, 회귀계수: a, b)
- 실제 값은 Y= aX1 +b + Error(오류 값, 잔차)이 될 것이며, Error를 최소로 하는 모델이 최적 회귀 모델임
- 전체 데이터의 잔차 합이 최소가 되는 모델을 만든다는 의미

- 오류 값은 +,-를 포함하므로 단순히 더하지 않고 절댓값을 취해서 더하거나(Mean Absolute Error), 오류 값의 제곱을
구해서 더하는 방식(RSS, Residul Sum of Square) 일반적임
- Error^2 = RSS
- RSS는 변수가 a, b인 식으로 표현 가능

- 회귀에서 RSS는 비용(Cost)이며, 회귀 계수로 구성되는 RSS는 비용 함수
- 머신러닝에서는 비용 함수가 반환하는 값을 지속해서 감소시키고 더 이상 감소하지 않는 최소의 오류 값을 구하는 것
- 비용 함수는 손실 함수(Loss Fuction)라고 부르기도 함
8.3 비용 최소화 - 경사 하강법(Gradient Descent)
- 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 회귀 계수를 보정함
- 미분값(접선의 기울기)이 감소하는 방향으로 회귀 계수를 보정하며 미분값이 최소인 지점의 회귀 계수를 반환
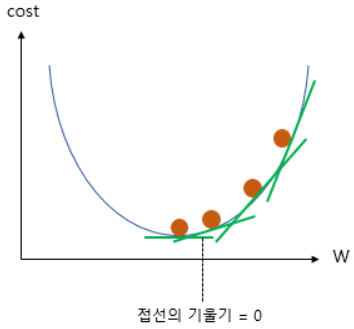
- 앞서 언급한 RSS 함수를 회귀 계수(w)로 표현 해 보면,

- w0, w1로 편미분

- 업데이트 시 편미분 값이 너무 클 수 있기 때문에 보정계수(여기선 알파)를 사용

- 파이썬 코드로 예시 확인



- 시간이 오래 걸린다는 단점
- 대부분 확률적 경사 하강법(Stochastic Gradient Descent)을 활용
- w 업데이트 시 전체 데이터가 아닌 일부 데이터(배치)를 이용한다는 차이점


8.4 LinearRegression을 이용한 보스턴 주택 가격 예측
- 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현
- fit() 메서드로 X, y 배열을 입력받으면 회귀 계수 W를 coef_ 속성에 저장
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)
1. fit_intercept → Default=True, y절편 값을 계산할지 말지 결정
2. normalize → Default=False, fit_intercept = False일 때는 무시, True일 때는 데이터 세트 정규화 결정
3. 속성값(coef_) → fit()을 수행했을 때 회귀 계수가 배열 형태로 저장하는 속성, (Target 값 개수, 피처 개수)
4. 속성값(intercept_) → 절편값
- OLS 추정 방식은 입력 피처의 독립성에 많은 영향을 받음
- 피처 간의 상관관계가 매우 높은 경우 분산이 커져 오류에 민감해짐(다중 공선성 문제, multi-collinearity)
- 상관관계가 높은 피처가 많을 경우
1. 독립적인 중요한 피처를 제외하고 제거 혹은 규제를 적용
2. PCA로 차원 축소를 수행
- 회귀 평가 지표
| 평가 지표 | 설명 | 수식 |
| MAE(Mean Absolute Error) | 실제 값과 예측값의 차이를 절댓값으로 평균 |  |
| MSE(Mean Squared Error) | 실제 값과 예측값의 차이를 제곱하여 평균 |  |
| RMSE(Root Mean Squared Error) | MSE에 루트를 씌운것(오류 크기 줄이기 위함) |  |
| R^2 | 분산 기반의 평가, 1에 가까울수록 정확도 높음 |  |
| 평가 방법 | 사이킷런 평가 지표 API | Scoring 함수 적용 값 |
| MAE | metrics.mean_absolute_error | 'neg_mean_absolute_error' |
| MSE | metrics.mean_squared_error | 'neg_mean_squared_error' |
| R^2 | metrics.r2_score | 'r2' |
- Scoring 함수 적용 값의 'neg'는 원래의 평가 지표 값에 '-1'을 곱하여 음수(Negative)를 만든 것
- 즉, 'neg_mean_absolute_error' = -1*metrics.mean_absolute_error
- 보스턴 주택 가격 예측

- 각 칼럼이 회귀 결과에 미치는 영향이 어느 정도인지 시각화
- Seaborn의 regplot() API 활용, X, Y축과의 산점도와 선형 회귀 직선 그려줌
- matplotlib.subplots() API 활용, 각 ax마다 칼럼과 PRICE 관계 표현
- ncols = 열 방향 그래프 개수, nrows = 행 방향 그래프 개수

- mean_squared_error(), r2_score() API 활용, MSE와 R2 Score 측정

- LinearRegression으로 생성한 주택 가격 모델의 intercept(절편)과 coefficients(회귀 계수)
- intercept_ 속성, coef_ 속성


- 최적화 수행(5개의 폴드 세트에서 cross_val_score() 교차검증)

'코딩 > Machine Learning' 카테고리의 다른 글
| 10. 회귀(Regression)_3 (0) | 2021.01.02 |
|---|---|
| 9. 회귀(Regression)_2 (0) | 2021.01.01 |
| 7. 분류(Classification)_3 (0) | 2020.12.13 |
| 6. 분류(Classification)_2 (0) | 2020.12.13 |
| 5. 분류(Classification)_1 (0) | 2020.12.10 |




댓글