11. 차원 축소(Dimension Reduction)

권철민 저, '파이썬 머신러닝 완벽 가이드', 2019.02.28

내 맘대로 요약 공부 중(문제시 비공개 및 삭제)

최초 작성일 2021.1.3

11.1 차원 축소(Dimension Reduction) 개요

- 대표적인 알고리즘 PCA, LDA, SVD, NMF

- 매우 많은 피처로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 데이터 세트를 생성하는 것

- 왜 하는가? [수많은 피처로 구성된 데이터의 예측 신뢰도 < 적은 피처로 구성된 데이터의 예측 신뢰도]

- 피처가 많을 경우 개별 피처간 상관관계가 높을 가능성이 큼

- 선형 회귀 등 선형 모델에서는 입력 변수 간의 상관관계가 높을 경우 다중 공선성 문제로 예측 성능 저하 우려 있음

- 즉, 매우 많은 다차원의 피처를 차원 축소하여 피처 수를 줄이면 더 직관적으로 데이터를 해석할 수 있음

- 차원 축소 후 데이터의 크기가 줄어들어 학습 수행이 원활해짐

- 피처 선택(feature selection) : 종속성이 강한 불필요한 피처는 제거, 주요 피처만 선택 

- 피처 추출(feature extraction)

• 기존 피처를 저차원의 중요 피처로 압축하여 추출(압축되면서 완전히 다른 값이 됨)
• 피처 추출은 피처를 함축적으로 더 잘 설명할 수 있는 또 다른 것으로 매핑하여 추출하는 것임
• 기존 피처가 인지하기 어려웠던 잠재적인 요소(Latent Factor)를 추출하는 것

- 이미지 데이터에서 잠재된 특성을 피처로 추출하여 과적합(Overfitting)을 방지

- 텍스트 데이터에서 단어들의 구성에서 잠재된 특성(숨겨진 의미)을 추출

 

11.2 PCA(Principle Component Analysis)

- 가장 대표적인 차원 축소 기법

- 여러 변수 간의 상관관계를 이용해 이를 대표하는 주성분(Principle Component)을 추출하여 차원을 축소

- 기존 데이터의 정보 유실이 최소화돼야 함 → 가장 높은 분산을 가지는 데이터의 축을 찾아 차원을 축소

생성된 벡터 축에 원본 데이터를 투영

1. 가장 큰 데이터 변동성(Variance)을 기반으로 첫 번째 데이터 축을 생성
2. 두 번째 데이터 축은 첫 번째 데이터 축에 직각이 되는 벡터(직교 벡터)로 생성
3. 세 번째 데이터 축은 두 번째 데이터 축에 지각이 되는 벡터로 생성... 반복
4. 생성된 데이터 축에 원본 데이터를 투영하면 벡터 축의 개수만큼의 차원으로 원본 데이터가 축소됨

---

- 입력 데이터의 공분산 행렬(Covariance Matrix)을 고유값 분해하여 구한 고유벡터에 입력 데이터를 선형 변환

- 고유벡터는 PCA의 주성분 벡터(입력 데이터의 분산이 가장 큰 방향)

- 고유값(Eigenvalue)은 고유벡터의 크기이며 입력 데이터의 분산

 

- 공분산은 두 변수 간의 변동을 의미( Cov(X,Y) > 0은 X가 증가할 때 Y도 증가한다는 의미)

- 즉, 공분산 행렬은 여러 변수와 관련된 공분산을 포함하는 정방형 행렬임

	X	Y	Z
X	1	4.5	2.7
Y	4.5	2	-3.4
Z	2.7	-3.4	3

- 대각선 원소는 각 변수(X, Y ,Z)의 분산, X와 Y의 공분산 4.5, X와 Z의 공분산 2.7, Y와 Z의 공분산 -3.4

 

- 고유벡터는 행렬 A를 곱해도 방향이 변하지 않고 크기만 변하는 벡터(Ax = ax / A는 행렬, x는 고유벡터, a는 스칼라값)

- 고유벡터는 여러 개가 존재, 정방행렬은 최대 그 차원 수 만큼의 고유벡터가 있음(2x2는 두 개, 3x3은 세 개)

 

- 공분산 행렬은 정방행렬(Diagonal Matrix)이며, 대칭행렬(Symametric Matrix)

- 대칭행렬은 항상 고유벡터를 직교행렬(Orthogonal Matix)로, 고유값을 정방 행렬로 대각화할 수 있음

- 입력 데이터의 공분산 행렬 C, n × n 직교행렬 P, n × n 정방행렬 ∑, 전치 행렬 P^T

- 고유벡터 행렬과 고유값 행렬로 대응

맨 오른쪽 괄호가 이상하긴한데 이해하길 바람

- 공분산 C = 고유벡터 직교 행렬 * 고유값 정방 행렬 * 고유벡터 직교 행렬의 전치행렬

- en은 n번째 고유벡터, ∂n은 n번째 고유벡터의 크기

- e1은 가장 분산이 큰 방향을 가진 고유벡터, e2는 e1에 수직이면서 두번째로 분산이 큰 방향을 가진 고유벡터

- 즉, 입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해 되며 분해된 고유벡터를 이용해 입력 데이터를

  선형 변환하는 방식이 PCA

1. 입력 데이터 세트의 공분산 행렬을 생성
2. 공분산 행렬의 고유벡터와 고유값을 계산
3. 고유값이 가장 큰 순으로 K개만큼 고유벡터 추출
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 입력 데이터를 선형 변환

- 많은 속성으로 구성된 원본 데이터를 핵심을 구성하는 데이터로 압축하는 것

- 붓꽃 데이터를 활용한 예시

데이터 불러오기

데이터 분포 시각화

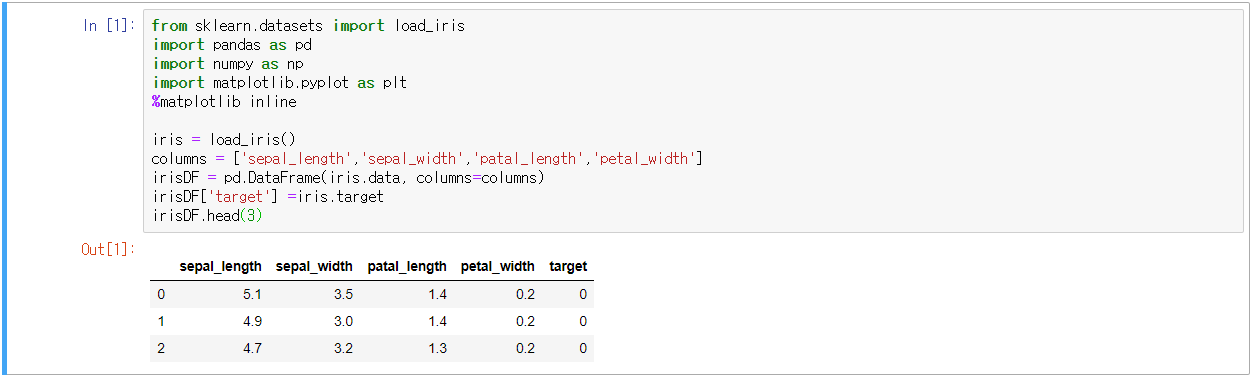
- PCA로 4개의 속성을 2개로 압축한 뒤, 2개의 PCA속성으로 데이터 분포 시각화

- 평균이 0, 분산이 1인 표준 정규 분포로 데이터 전처리

Sklearn의 StandardScaler 이용

fit(), transform() PCA 변환 수행

DataFrame으로 변환하여 데이터 확인

PCA 변환 데이터 세트가 원본 데이터 세트 보다 더 분리가 잘 되어 있음

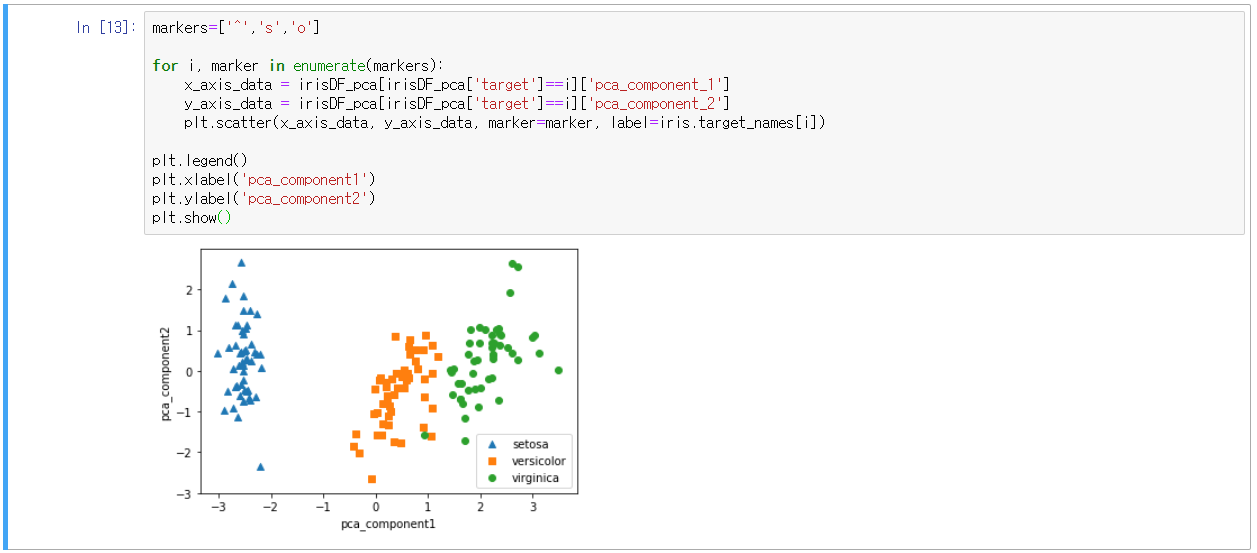
- 첫 번째 축인 pca_component_1이 원본 데이터의 변동성을 잘 반영했음

- component별 변동성 비율 확인 : explained_variance_ratio_

첫 번째축이 변동성의 76% 이상을 표현

- 원본 데이터와 PCA 변환 데이터를 사용한 랜덤포레스트 결과 성능 비교

PCA 변환 후 성능이 더 좋아짐, 일반적으로 쉽게 성능이 좋아지지 않음

- 조금 더 많은 피처를 갖는 데이터를 활용

- https://archivearchive.ics.uci.edu/ml/datasets/default+of+credit+card+clients

UCI Machine Learning Repository: default of credit card clients Data Set

데이터 불러오기

칼럼명 정리

DataFrame의 corr() 속성을 활용하여 각 속성간의 상관도를 구하여 히트맵 시각화

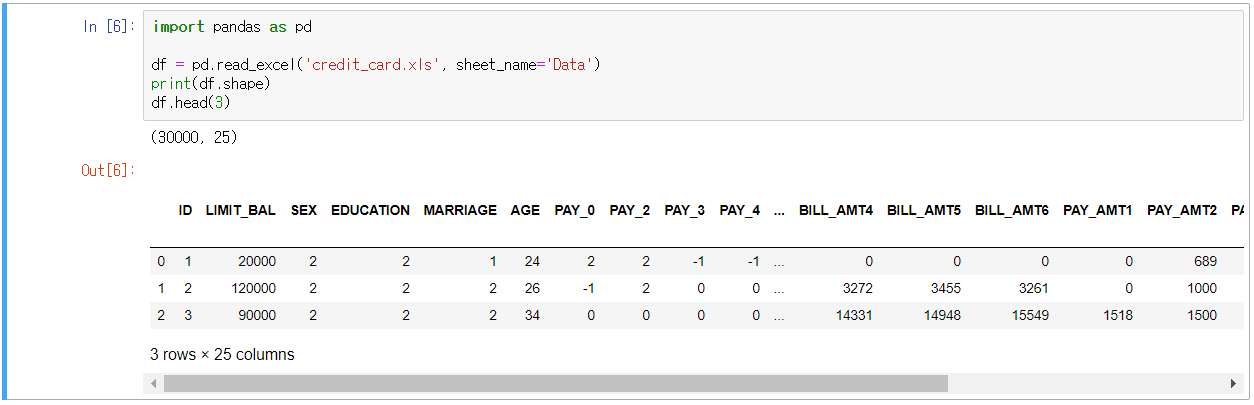
- annot=True : 각 셀에 숫자를 표시하는지 여부 , fmt: '.1g' : 'd'는 정수 표시하라는 것인데 .1g는 찾아도 잘 안 나옴(아마 0이 아닌 첫 번째 숫자 이하 반올림)

BILL_AMT1 ~ BILL_AMT6 속성 끼리의 상관관계 높음, PAY_1~PAY_6 속성 끼리의 상관관계 높음

- BILL_AMT1 ~ BILL_AMT6까지 6개의 속성을 2개의 컴포넌트로 PCA 변환하여 변동성 확인

2개의 Component로 6개의 속성 변동성을 95% 식별 가능, 첫번째 축으로 90% 변동성 식별 가능

- 원본 데이터와 PCA 변환 데이터의 분류 예측 결과 비교

원본 데이터

PCA 변환 데이터

- PCA 변환 데이터로 원본 데이터의 성능이 나온다는 것은 그만큼 데이터 압축이 잘 이루어졌다는 것

11.3 LDA(Linear Discriminant Analysis)

- 선형 판별 분석법, 지도학습임(fit 메서드를 호출할 때 target 값을 입력해줌)

- PCA와 유사하지만 LDA는 분류(Classification)에서 사용하기 쉽도록 분별 기준을 유지하면서 차원을 축소함

- LDA는 입력 데이터의 결정 값 클래스를 최대한 분리할 수 있는 축을 생성

- 클래스 간 분산(between class scatter), 클래스 내부 분산(within class scatter)의 비율을 최대화하는 방식

- 클래스 간 분산은 최대한 크게, 클래스 내부 분산은 최대한 작게

1. 클래스 간 분산, 클래스 내부 분산 행렬을 구함(개별 피처의 mean vactor 기반)
2. 클래스 내부 분산 행렬 Sw, 클래스 간 분산 Sb, 고유벡터로 분해
3. 고유값이 가장 큰 순으로 K개 추출(LDA변환 차수 만큼의 수)
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 입력 데이터를 변환

고유 벡터로 분해

- 붓꽃 데이터를 활용한 예시

데이터 불러오기 + 2개의 Component로 LDA 변환

시각화

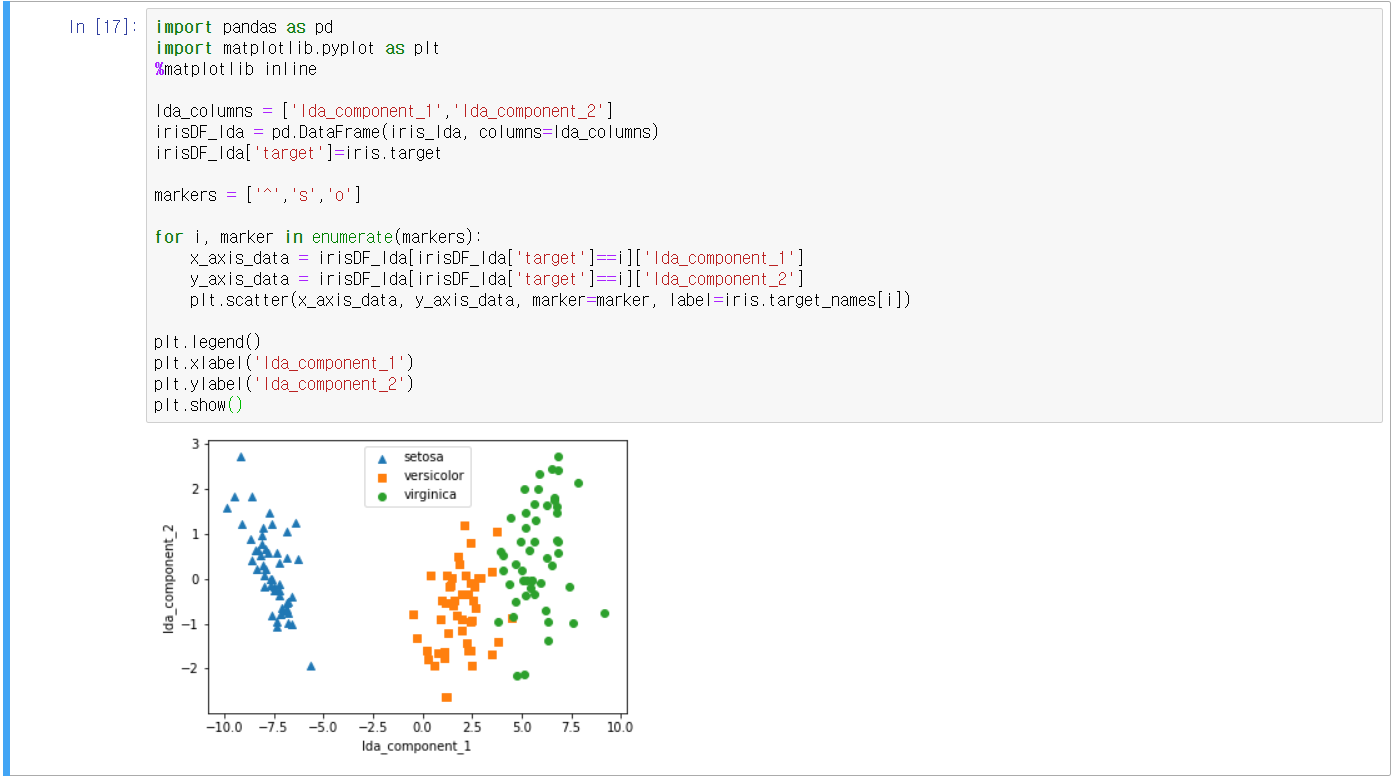
11.4 SVD(Singular Value Decomposition)

- 특이값 분해

- PCA와 유사하지만 SVD는 정방행렬뿐만 아니라 행과 열의 크기가 다른 행렬도 적용 가능

- m×n 행렬 A, ∑ 대각행렬, 특이벡터 U, V

- 모든 특이벡터(Singular vector)는 서로 직교하는 성질이 있음

- A가 m×n일 때, U는 m×m, ∑는 m×n, V는 n×n

- 하지만 SVD는 행렬의 차원을 줄인 형태로 적용(A가 m×n일 때, U는 m×p, ∑는 p×p, V는 p×n)

원본 행렬에서 차원을 줄인 형태로 SVD 적용

① 넘파이(Numpy)의 SVD를 활용한 예제

랜덤하게 4x4 행렬 생성

- U matrix, Sigma Value, V Transpose matrix 확인

클래스 속성으로 쉽게 확인 가능

- 분해된 U matrix, Sigma Value, V Transpose matrix를 원본 행렬로 복원(내적)

- Sigma의 경우 0이 아닌 값을 1차원으로 추출한 것이기 때문에 0이 포함된 대칭행렬로 변환하여 진행

원본 행렬과 동일하게 복원

- 데이터 세트에 로우 간 의존성이 있을 경우 값의 변화 확인

로우(행) 끼리의 연관이 깊어짐

차원 자체는 변하지 않았으나, Sigma 값 중 두 개가 0으로 변함

- Sigma 값 중 두 개가 0으로 변한 것은 선형 독립인 행 벡터의 개수가 2개라는 뜻

- Sigma 값의 선행 두 개만 0이 아니므로.. U행렬 중 선행 두 개의 열만 추출, Vt행렬 중 선행 두 개의 행만 추출

복원이 잘된것을 확인

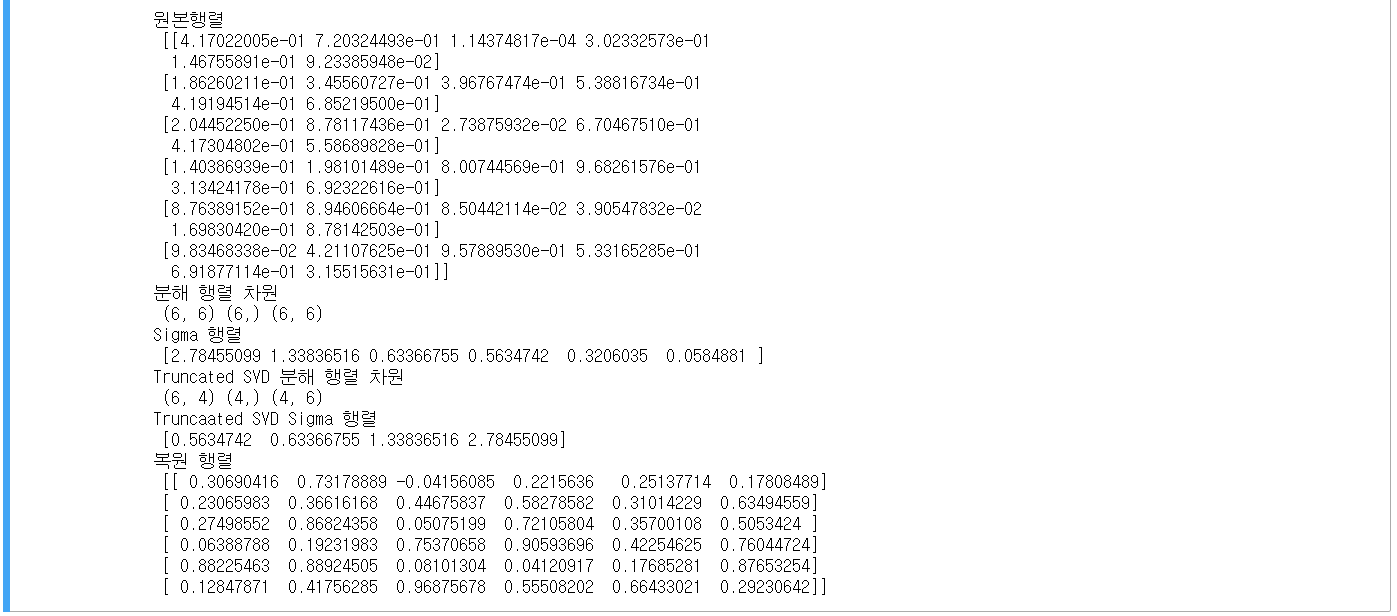
② Truncated SVD를 활용한 예제

- ∑행렬의 대각원소 중 상위 일부 데이터만 추출하여 분해

- 더 작은 차원으로 분해하는 것이기 때문에 원본 행렬을 정확하게 복원할 수 없음

- 데이터 정보가 압축되어 분해되지만 상당하게 원본 행렬을 근사할 수 있음(성능 좋다는 얘기)

- scipy의 svds 활용

원본으로 행렬 차원을 확인, Truncated SVD로 행렬 차원 확인

완벽하게 원본 행렬을 복원하지 못하고 근사한다

③ 사이킷런 TruncatedSVD 클래스를 이용한 변환

- PCA와 유사하게 fit(), tranform()을 호출하여 차원 축소 변환

- 붓꽃 데이터 예시

SVD도 훌륭하다

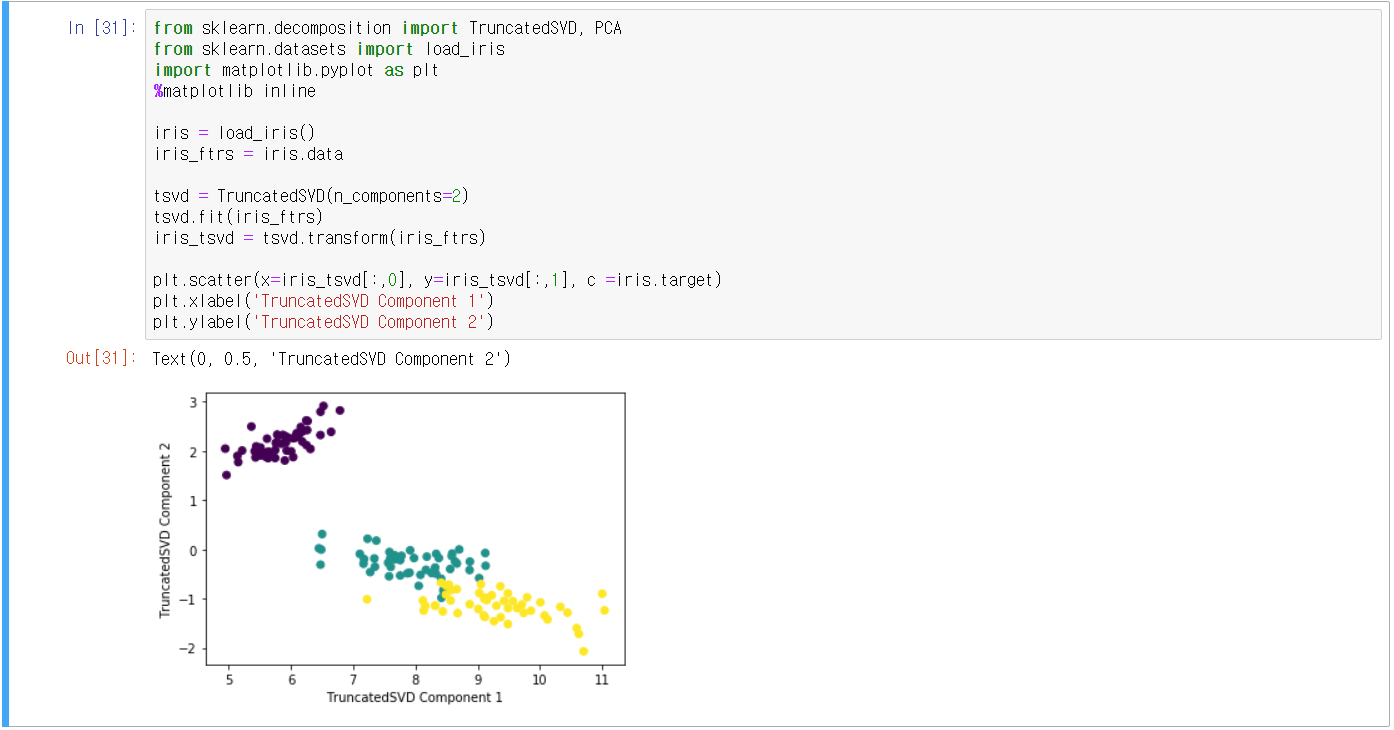
- PCA vs SVD 비교

거의 동일하다

- 데이터 세트가 스케일링되면, PCA와 SVD는 거의 동일한 성능을 구현함

11.5 NMF(Non-Negative Matrix Factorization)

- 낮은 랭크 행렬 근사(Low-Rank Approximation) 방식

- 원본 행렬 내의 모든 원소 값이 양수(0 이상)이면, 아래와 같이 분해될 수 있다는 것

행렬 분해(Matrix Factorization)

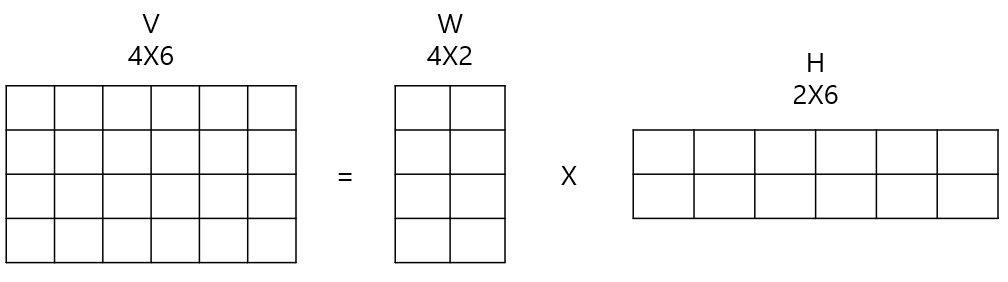
- 분해 행렬 W: 원본 행의 잠재 요소에 대한 대응

- 분해 행렬 H: 원본 열의 잠재 요소에 대한 대응

- 붓꽃 데이터 예시

분류가 잘 되는 편

- 잠재된 요소를 추출하여 분류하기 때문에, 잠재 요소(Latent Factoring) 기반의 추천 방식에 주로 사용

 

- 차원축소를 하는 이유는

1. 수많은 피처를 갖고 있는 데이터 세트의 피처 수를 줄이기 위함
2. 피처를 압축하여 피처들이 갖고 있는 잠재적인 요소를 추출 및 파악하기 위함(어떤 문장에서 내면의 뜻이라던지..)
3. 학습 데이터의 크기를 줄여 학습 효율을 증가시키기 위함